Bienvenido a nuestra sección dedicada a profundizar en temas informáticos de creciente interés, complejos al grado en el que el programador estandar tiene dificultades en alcanzar.En el día de hoy estaremos evaluando:
Versión y Revisión de los Ensamblados
Por Bison
Por Bison
Estimados:
Cuando nos encontramos trabajando con proyectos de ...(Censurado), es bien sabido que ustedes son unos perros para darle número de versión y revisión, es más, ustedes no laburan si no fuera por mi dado que yo soy el único capacitado enchufarle al ensamblado un número natural al final, seguido de un punto y luego otro número natural.
Como Café Pa' Negros no necesita azucar, no voy a andar explicandoles una y otra vez como hacer esta pavada de versión y revisión que a mi me lleva casi 12 segundos y que.. por supuesto, esta en todos los proyectos que yo he realizado, inclusive desde antes de que abriera la Empresa.
Aca les va la explicación que solo yo, Mr.Bison, soy capaz de entender, reformular y modificar en base a lo que más o menos se me antoja.. esto es porque soy Ingeniero, yo programaba con una aguja sobre un chip cuando tenia 4 años en los intervalos mientras jugaba en el jardin con mis compañeritos, esto es porque claro.. soy un salado... :
Sea f integrable sobre [a,b] y
Cuando nos encontramos trabajando con proyectos de ...(Censurado), es bien sabido que ustedes son unos perros para darle número de versión y revisión, es más, ustedes no laburan si no fuera por mi dado que yo soy el único capacitado enchufarle al ensamblado un número natural al final, seguido de un punto y luego otro número natural.
Como Café Pa' Negros no necesita azucar, no voy a andar explicandoles una y otra vez como hacer esta pavada de versión y revisión que a mi me lleva casi 12 segundos y que.. por supuesto, esta en todos los proyectos que yo he realizado, inclusive desde antes de que abriera la Empresa.
Aca les va la explicación que solo yo, Mr.Bison, soy capaz de entender, reformular y modificar en base a lo que más o menos se me antoja.. esto es porque soy Ingeniero, yo programaba con una aguja sobre un chip cuando tenia 4 años en los intervalos mientras jugaba en el jardin con mis compañeritos, esto es porque claro.. soy un salado... :
Sea f integrable sobre [a,b] y
-
-
- Entonces
![m \leq f(x) \leq M \forall x \in [a,b]](http://upload.wikimedia.org/math/0/3/8/038b42a32b280aad43eb4056a7e6c3d4.png)
Demostración
Hipótesis:
- Sea
. - Sea f función integrable sobre el intervalo [a,b] y continua en c.
- Sea F una función sobre [a,b] definida así:
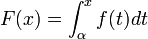con ![\alpha \in [a,b]](http://upload.wikimedia.org/math/d/f/4/df48605dc02c8a270608ea1a3435d4f1.png)
Tesis:
- F'(c)=f(c)
Por definición se tiene que 
.
Sea h>0. Entonces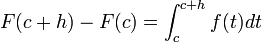 
.
Se define mh y Mh como:
-
,
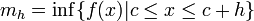Aplicando el 'lema' se observa que
-
.
Por lo tanto,
Sea h <>. Sean
-
,
.
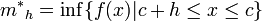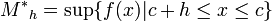Aplicando el 'lema' se observa que
-
.
Como
-
,
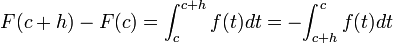entonces
-
.
Puesto que h <>, se tiene que
-
.
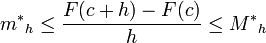Y como f es continua en c se tiene que
-
,
y esto lleva a que
-
-
.
-
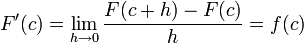Ejemplos
Fin de la demostración
Pero señores, dado que son unos reverendos PERROS y unos completos Usuarios, les voy a explicar de una forma que ustedes entiendan:
Cuando modifiquen un ensamblado, lo primero es versión y lo segundo es revision, si no es compatible para atras entonces cambia la versión, si lo es, entonces cambiará la revisión.
Cuando modifiquen un ensamblado, lo primero es versión y lo segundo es revision, si no es compatible para atras entonces cambia la versión, si lo es, entonces cambiará la revisión.
No hay discusión.... Mamita los cabezudos...
Gracias
*******************
*******************
Este fue otro aporte de Mr. Bison a la comunidad Informática.
(Gracias Carrymap)
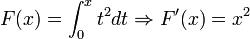
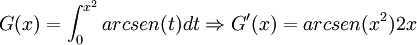
3 comentarios:
La novia GPS no tiene problema con lo de taxi boy... Si nos ponemos de acuerdo con los números, claro...
Ahora, siendo objetivos...
Quien va a pagar por Uds???
Busquen por otro rubro mejor =P
Solo quiero aprovechar este medio para decir que ODIO PROFUNDAMENTE a (Censurado) y semejantes...
Piensen... Siempre puede pasar que se dinamite algo o que Bison aparezca muerto... Lo ODIOOOOOOOOOOOOOOOOOOOOOO!!!
Gracias, me voy a tomar la pastilla...
Publicar un comentario